数据分析的基石-----------统计学

数据分析是指用适当的统计分析方法对收集来的大量数据进行分析，将它们加以汇总和理解并消化，以求最大化地开发数据的功能，发挥数据的作用。因而数据分析的基石便是统计学。而关于统计学，我们可以观看BBC的纪录片《The Joy of stats》，从中我们能够意识到统计学的强大魅力，统计学已经应用到我们生活的方方面面，各行各业都利用统计学方法处理数据。

数据分析的工具基础-----------计算机科学和数学

数据分析的数学基础在20世纪早期就已确立，但数据分析经常会面对大量的数据，所以直到计算机的出现才使得实际操作成为可能，并使得数据分析得以推广。

学习统计分析的意义

现代社会，随着科学技术的发展以及人类社会活动的发展，各行各业复杂的数据混杂在一起，如何理性的客观的认识世界，如何将海量的数据为人类所用，更好的促进社会生活发展，我想现在我们完全可以利用计算机科学和数学运用统计学知识分析数据，寻找规律，理解数据背后的故事。就比如我很想统计出历年来五一假期从上海去南京车流量的多少，计算出五一开车自驾到南京的时间于与平时的差异，然后判断去南京究竟选择哪一种出行方式。

统计学分析方法多种多样，本次讲述其中一种描述性统计分析。

描述统计学

描述性统计，是指运用制表和分类，图形以及计算概括性数据来描述数据特征的各项活动。（简单来说，就是用一些直观的表格，图形，概括性数据来表达数据。）

当我们在面对多条数据组合而成的数据集，复杂的数据往往不能让我清楚认识这组数据的基本特征，这个时候我们就需要几个关键指标代替描述数据集的整体情况。以下介绍描述数据集的四个指标，平均值，四分位数，标准差，标准分。

一、平均值

平均数是统计学中最常用的统计量，用来表明资料中各观测值相对集中较多的中心位置。统计平均数是用于反映现象总体的一般水平，或分布的集中趋势。

优点：用平均数表示一组数据的情况，有直观、简明的特点。

缺点：缺点是易受到极端数据的影响，对异常数据不敏感。

二：四分位数

四分位数也称为四分点，是指在统计学中把所有数值由小到大排列并分成四等分，处于三个分割点位置的数值,即数据排序后处于25%、50%、75%位置上的值。

首先介绍中位数

对于有限的数集，可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个，通常取最中间的两个数值的平均数作为中位数。

将n个数从小到大排列：

Q2=n个数组成的数列的中位数（Median）；

当n为奇数时，中数Q2将该数列分为数量相等的两组数，每组有 (n-1)/2 个数，

Q1=第一组 (n-1)/2 个数的中数，

Q3=第二组(n-1)/2个数的中数；

当n为偶数时，中数Q2将该数列分为数量相等的两组数，每组有n/2数，

Q1=第一组 n/2个数的中数，

Q3=为第二组 n/2 个数的中数；

不论Q1，Q2，Q3的数值为何，均视为一个分界点，以此将总数分成四个相等部份，可以通过Q1，Q3比较，分析其数据变量的趋势。

四分位数在统计学中的箱线图绘制方面应用也很广泛。所谓箱线图就是 由一组数据5个特征绘制的一个箱子和两条线段的图形，这种直观的箱线图不仅能反映出一组数据的分布特征，而且还可以进行多组数据的分析比较。这五个特征值，即数据的上界，下届，中位数以及上下四分位数。

箱线图示意，可看出中位数靠近下四分位数

应用

1、箱线图常用来比较不同类别数据集的整体情况，可使用python绘制。

2、四分位数能收在数据集中识别出可能的异常值，运用Tukeys Test方法。

当我们对数据集进行分析的时，首先我们先采用一定的技术手段找出异常值，并且对找出的异常值的准确性要进一步检查以确定如何处理异常值。

异常值可能出现如下几种情况：

被错误标记的数值，需要我们进一步修改数值；

被错误包含在数据集中的数值，需要删除数据；

反常的数据但是被正确的记录在数据集中,这种数据需要保留。

那么我们如何找出异常值呢，这里我们可以采用Tukeys Test方法：

最小估计值：Q1- k(Q3-Q1) 最大估计值：Q3 - k(Q3 - Q1)

k为常量，k =1.5 中度异常，k=3 极度异常

超过最小估计值和最大估计值范围就有可能是异常值，可以根据不同情况，对K进行取值。

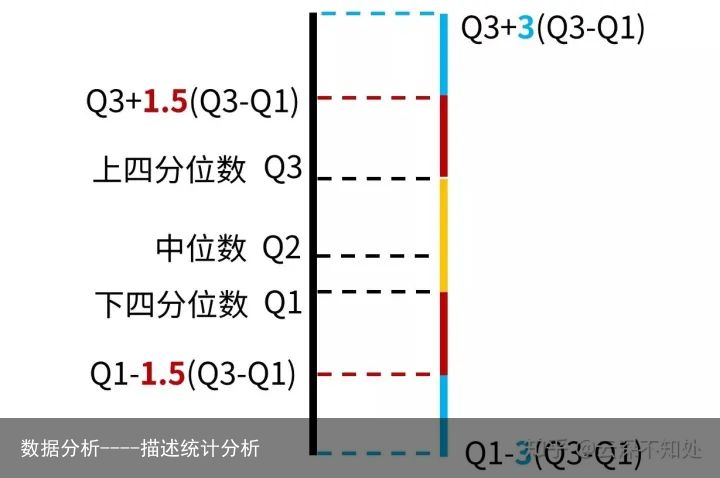Tukey's Test方法，超过最大最小估计值范围就有可能是异常值，此图需要记牢

四分位数的优点：从整体上描述出数据集的分布。

四分位数的缺点：无法告知数据的波动有多大。

三、标准差

当我们需要知道某个数据集是否稳定的时候，就是想知道这个数据集的波动大小，也就是数据集之间偏离平均值的程度，又称为离散程度、变异性。

这里我们引入一个指标，标准差。

标准差又称为均方差。在概率统计中最常使用作为统计分布程度上的测量。标准差是方差的算是平方根。它能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。

数据集： 、、x1、x2、x3...xnx_{1} 、x_{2}、x_{3}... x_{n}

平均值： μ\mu

标准差 （）σ（μ）=1n∑i=1n(xi−μ)2\sigma（\mu）=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(x_{i}-\mu)^{2}}}

标准差描述了一个数据集在整体变化中偏离平均值的幅度也就是波动大小。标准差的单位与相应计算数据的单位相同。标准差数值越大，数据集整体的偏离程度越大，标准差数值越小，数据集整体的偏离程度越小。

标准差优点：表示数据整体的波动大小。

标准差缺点:如果两个数据集差别比较大，那么就无法比较。

如果能用标准差除以数据集的平均值，就可以消除数据大小的差异，这里我们引入概念变异系数，通常用变异系数来比较不同数据集的波动大小。

变异系数=标准差/平均值。

应用：股票基金选择

四、标准分

标准分又称为z分数或标准化值。标准分，是一种由原始分推导出来的相对地位量数，它是用来说明原始分在所属的那批分数中的相对位置的。

数据集： 、、x1、x2、x3...xnx_{1} 、x_{2}、x_{3}... x_{n}

平均值： μ\mu

标准差： σ\sigma

标准分: z=xn−μσz = \frac{x_{n}-\mu}{\sigma} ( xnx_{n} 为具体的某个数值）

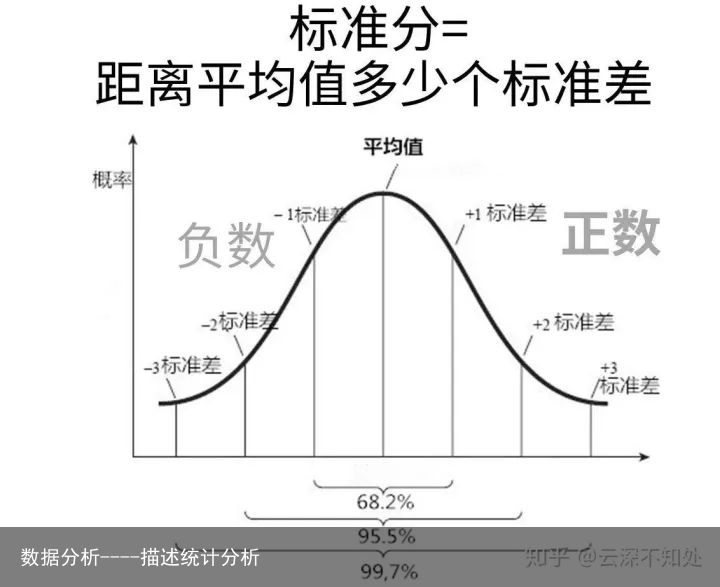正态分布中标准差的运用

标准分 = 距离平均值多少个标准差，通过标准分可以知道数值与平均值的相对接近程度。

应用

用6西格玛理念提高质量管理，6西格玛 = 标准分等于6

总结知识点

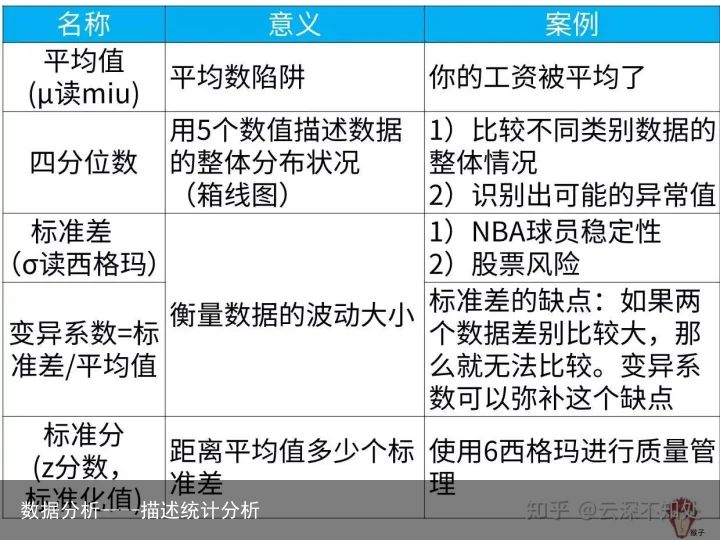知识点汇总

熟悉数据集

数据集来源

Baby Goods Info Data-数据集-阿里云天池​tianchi.aliyun.com/dataset/dataDetail?dataId=45&userId=1

<表1.购买商品> <表2.婴儿信息>

1）表1购买商品字段

user_id:用户id，一个ID对应一个用户；

auction_id:物品编号（item_id）；

cat_id: 商品种类ID（商品二级分类，表示商品属于哪个类别）；

cat1: 商品种类ID（商品一级分类，表示商品属于哪个类别）；

（cat1和cat_id分别是商品的一级分类和二级分类，比如上衣和衣服，汽车和玩具汽车这样的关系。虽然都是数字串id，但是根据这层关系，就可以用数据透视表来展示逻辑关系。比如商品大类下面，哪个分类更畅销）；

property:商品属性（属性值可以是大小，可以是尺码、毫升等数字，还可以指品牌等，一切可以描述商品特征的都可以称为属性值）；

buy_mount ：每次交易所购买的数量；

day：每次交易的时间。

bigint为Transact-SQL的系统数据类型，当整数值超过int数据范围时才可以使用。bigint可以精确的表示从-2^63到2^63-1(即从-9,223,372,036,854,775,808到 9,223,372,036,854,775,807)之间的整数，它占用了八个字节的存储空间。

从表1中我的思考：

1、平均每个消费者每年买多少婴儿用品？

婴儿用品销量求和/年份/用户数量。可以结合每一年新生儿出生数量，预判销售量。

2、一级分类中哪种是销售量最好，哪种最差？各一级分类的销售数据集的整体分布情况？

对各一级分类分别计算出交易量之和，由小到大进行排序，求出四分位数，画出箱线图，排除可能的异常值，能够直观判断出某一级分类是否畅销。

3、各一级分类销售情况是否稳定？哪一种最稳定？

先计算各一级商品总的销售量，算出此数据集的四分位数，判断是否此数据集的差别是否过大，进而分析是否需要用变异系数的方法判断销售量的波动大小。

4、某种属性的商品销售量相对满足市场要求？

按照属性分类，分别求和，对得到的数据集求标准分，通过对标准分的比较能够知道哪种属性更接近市场需求。

2）表2婴儿信息表字段

user_id:用户id

birthday:出生日期

gender:性别（0女性；1男性；2未知的性别）

从表2中我的思考：

1、各年份，男女婴儿的对婴儿用品的需求是否有波动？各性别数量的波动情况？

以各年份婴儿人数的总量为数据集，计算标准差，判断男生，女生在这几年中对婴儿婴儿用品的需求是否有较大的波动。

2、两种性别相比较，是男婴儿购买力数量多还是女婴儿购买数量多？

这需要结合两个表格，因为id的唯一性，我们可以通过某种方式得到对应id的购买数量，再分别计算出总量，求男女购买力的平均数。

【下一关希望可以解决的问题】：

对着正规的分析方法去比较，不断修正和改进自己的分析思维。