一个多元逻辑回归的例子

和一般的回归一样，逻辑回归可以有定性预测变量与定量预测变量。书上用了母鲎及其追随者的例子来阐述这里的分析。

注：关于鲎，可以看《地理中国》的科普《地理·中国》 20200424 奇水谜岛 5。

利用宽度与颜色作为预测变量的模型构建

使用母鲎的宽度以及颜色作为预测变量。母鲎的颜色有5个类别：light，medium light，medium，medium dark，dark。由于样本中并没有颜色为“light”的鲎，所以我们的模型仅仅含有其余的4个类别。

我们将颜色当做属性预测变量，用三个指示变量去描述这4个类别。模型为

logit[P(Y=1)]=α+β1c1+β2c2+β3c3+β4xlogit[P(Y=1)]=\alpha+\beta_1c_1+\beta_2c_2+\beta_3c_3+\beta_4x

其中 xx 代表宽度， c1c_1 代表颜色"稍浅"， c2c_2代表颜色“中等”，c3c_3 代表颜色“稍深”。 c1=c2=c3=0c_1=c_2=c_3=0 代表颜色为“深”。

> library(cdabookdb) > library(dplyr) > data("horseshoecrabs") > horseshoecrabs=horseshoecrabs%>% + mutate( + Color.factor=factor(Color,4:1), + psat=as.integer(horseshoecrabs$Satellites>0) + ) > m1=glm( + psat~Width+Color.factor,data=horseshoecrabs,family=binomial() + ) > summary(m1) Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -12.7151 2.7617 -4.604 4.14e-06 *** Width 0.4680 0.1055 4.434 9.26e-06 *** Color.factor3 1.1061 0.5921 1.868 0.0617 . Color.factor2 1.4023 0.5484 2.557 0.0106 * Color.factor1 1.3299 0.8525 1.560 0.1188 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Null deviance: 225.76 on 172 degrees of freedom Residual deviance: 187.46 on 168 degrees of freedom

logit[P^(Y=1)]=−12.715+0.468x+1.11c3+1.40c2+1.33c1logit[\hat{P}(Y=1)]=-12.715+0.468x+1.11c_3+1.40c_2+1.33c_1

根据参数估计，我们可以知道，颜色为dark的鲎， c1=c2=c3=0c_1=c_2=c_3=0 ，预测的方程为 logit[P^(Y=1)]=−12.715+0.468xlogit[\hat{P}(Y=1)]=-12.715+0.468x ；颜色稍浅的鲎， c1=1c_1=1 ， logit[P^(Y=1)]=(−12.715+1.330)+0.468x=−11.385+0.468xlogit[\hat{P}(Y=1)]=(-12.715+1.330)+0.468x=-11.385+0.468x 。

模型假设不存在颜色和宽度之间的交互作用。对于所有颜色，宽度的效应相同—— P(Y=1)P(Y=1) 关于宽度的四条曲线形状相同。对于每种颜色，宽度增加 11 厘米， Y=1Y=1 的优势就变为 exp{0.468}=1.6exp\{0.468\}=1.6 倍。

两个颜色参数估计的差值在指数变换之后等于对比这两种颜色的优势比的估计值。

plot( NULL, xlim=c(18,34),ylim=c(0,1), slab="Width",ylab="Predicted Probability" ) sapply(1:4,function(i) { newdata=data.frame( Width=seq(17,35,0.1), Color.factor=as.character(i) ) pred_prop=predict(m1,newdata,type="response") points(newdata$Width,pred_prop,type="l",col=i) }) legend(28,0.4,col=1:4,legend=paste0("Color",1:4),lty=1)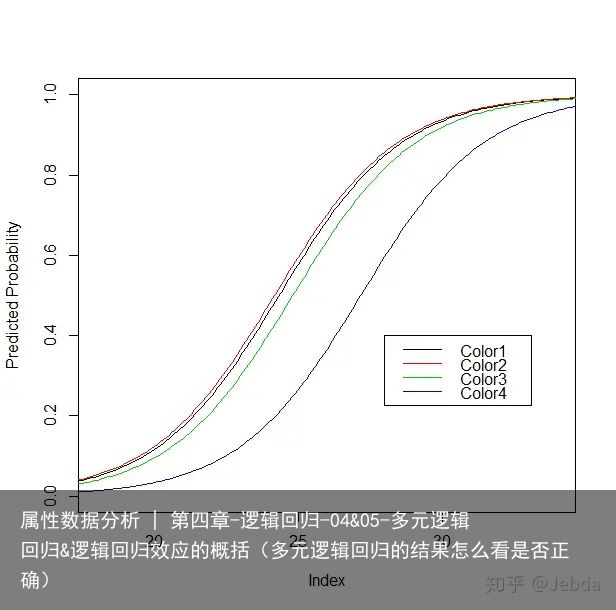

曲线在横轴上的平行性说明了任何两条曲线都不相交。颜色4——dark的母鲎具有追随者的概率估计值比其他颜色的母鲎都要低。

利用模型对比决定某一项的去留

接下来我们要做的事情，是确定颜色变量是否有必要引入。也就是说我们将检验 H0:β1=β2=β3=0H_0:\beta_1=\beta_2=\beta_3=0 ——控制宽度，存在追随者的概率与颜色无关。为了检验这个问题，我们可以将包含该项的模型的极大对数似然函数值 L1L_1 与不含该项的简单模型的极大对数似然函数值 L0L_0进行比较。于是我们拟合了含颜色项的模型与不含颜色项的模型，通过residual deviance得到−2(L0−L1)=194.45−187.46=6.99-2(L_0-L_1)=194.45-187.46=6.99 ， L1L_1模型自由度为171171 ， L2L_2 模型自由度为 168168 ，那么在 H0H_0 下，检验统计量近似 df=3df=3 的卡方分布，P值为 0.0720.072，给出了颜色效应的轻微证据。加上之前我们分析的深色母鲎的概率估计值与其它类相比有很大的差异，所以将颜色预测变量留在模型中更加安全。

需要注意的是，如果我们删除颜色变量，需要删除的是所有的颜色预测变量，而不是仅仅删除一个或者某两个。

有序预测变量的定量化处理

我们现在已经决定将颜色留在模型中了。由于颜色具有由浅至深的自然的类别顺序，我们之前的模型忽略了这一点。有一种简单的模型是将颜色处理为定量的。当指定每个类别的得分后，我们可以假设颜色对logit具有线性效应。

我们给颜色的打分如下： c={1,2,3,4}c=\{1,2,3,4\} ，并且拟合模型

logit[P(Y=1)]=α+β1c+β2xlogit[P(Y=1)]=\alpha+\beta_1c+\beta_2x

> m2=glm(psat~Color+Width,family=binomial(),data=horseshoecrabs) > summary(m2) Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -10.0708 2.8068 -3.588 0.000333 *** Color -0.5090 0.2237 -2.276 0.022860 * Width 0.4583 0.1040 4.406 1.05e-05 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Null deviance: 225.76 on 172 degrees of freedom Residual deviance: 189.12 on 170 degrees of freedom

得到的模型为 logit[P^(Y=1)]=−10.071−0.509c+0.458xlogit[\hat{P}(Y=1)]=-10.071-0.509c+0.458x ，颜色和宽度估计的 SESE 分别为 、0.224、0.1040.224、0.104，表明了两个变量都具有强烈的效应。对于给定的宽度，颜色每加深一个程度，具有追随者的优势的估计值将乘以exp{−0.509}=0.60exp\{-0.509\}=0.60——深色母鲎具有追随者的优势估计值是颜色稍深母鲎优势估计值的60%60\% 。

将这个模型与 L1L_1 进行比较我们可以得到似然比统计量为 189.12−187.46=1.66189.12-187.46=1.66 ，自由度为 df=2df=2，P值为0.44。这个似然比统计量检验的假设为：在已知每种颜色都具有单独参数的复杂模型成立的前提下，将颜色处理为定量的简单模型是成立的。我们没有理由去拒绝原假设，于是这样的线性简化看起来是可以接受的。

再回头看我们最初的模型：logit[P^(Y=1)]=−12.715+0.468x+1.11c3+1.40c2+1.33c1logit[\hat{P}(Y=1)]=-12.715+0.468x+1.11c_3+1.40c_2+1.33c_1 ，将颜色当做属性量表，效应的估计分别为： 1.33">c1−>1.33c_1->1.33 , 1.40">c2−>1.40c_2->1.40 , 1.11">c3−>1.11c_3->1.11 , 0">c4−>0c_4->0 。可以看出前三个类别的值更相似。于是我们可以重新将颜色变成二元变量——深色母鲎 c=0c=0 ，其余颜色 c=1c=1 。

> m4=glm( psat~is.dark+Width, family=binomial(), data=horseshoecrabs ) > summary(m4) Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -12.9795 2.7272 -4.759 1.94e-06 *** is.darkTRUE 1.3005 0.5259 2.473 0.0134 * Width 0.4782 0.1041 4.592 4.39e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Null deviance: 225.76 on 172 degrees of freedom Residual deviance: 187.96 on 170 degrees of freedom

这个二分得分模型与将颜色处理为名义量表的模型的似然比统计量为： 187.96−187.46=0.5187.96-187.46=0.5 ， df=2df=2 ，P值为 0.780.78 ，于是我们没有足够的证据去拒绝原假设——即我们认为这样的简化是足够的。

对于给定的宽度，颜色较浅的母鲎具有追随者的优势估计值是深色母鲎优势估计值的exp{1.300}=3.7exp\{1.300\}=3.7 倍。

所以，不论是将颜色转化为得分定量模型，还是将颜色转化为二分变量的模型都认为深色母鲎具有追随者的概率会小一些。

当几个模型的拟合相当时，我们会采用简单的模型，因为它更容易解释。

具有交互项的模型

一个更复杂的模型是：允许颜色与宽度的交互项存在。不同颜色下，宽度对出现追随者概率的曲线将不相同，所以两种颜色的对比会随着宽度值变化。我们这里将颜色变量变成二元的——深色母鲎c=0c=0 ，其余颜色 c=1c=1 。那么具有交互项的模型的预测方程为：

> horseshoecrabs$is.dark=as.character(horseshoecrabs$Color<4) > m3=glm( + psat~is.dark*Width, + family=binomial(), + data=horseshoecrabs + ) > summary(m3) Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -5.8538 6.6939 -0.874 0.382 is.darkTRUE -6.9578 7.3182 -0.951 0.342 Width 0.2004 0.2617 0.766 0.444 is.darkTRUE:Width 0.3217 0.2857 1.126 0.260 Null deviance: 225.76 on 172 degrees of freedom Residual deviance: 186.79 on 169 degrees of freedom

具有交互项的模型的预测方程为：

logit[P^(Y=1)]=−5.854−6.958c+0.200x+0.322(c×x)logit[\hat{P}(Y=1)]=-5.854-6.958c+0.200x+0.322(c\times x)

对于深色的鲎， c=0,logit[P^(Y=1)]=−5.854+0.200xc=0,logit[\hat{P}(Y=1)]=-5.854+0.200x ，

对于浅色的鲎， c=1,logit[P^(Y=1)]=−12.814+0.522xc=1,logit[\hat{P}(Y=1)]=-12.814+0.522x

在 x=21.6x=21.6 之后，颜色交浅的母鲎具有追随者的概率估计值更大。

这个模型与无交互项模型相比，

m4=glm(psat~is.dark+Width,family=binomial(),data=horseshoecrabs)

似然比检验统计量为： 187.96−186.79=1.17187.96-186.79= 1.17 ， df=1df=1，p值为0.279，交互项存在的证据并不强烈。尽管两种颜色的宽度效应的样本斜率差异很大，但是样本中仅仅具有24个深色的样本，所以深色的效应具有相对大的标准误。

逻辑回归效应的概括

通过与优势比有关的优势的乘积效应。这一点一直贯穿在我们之前的分析中。逻辑回归模型二元变量前的系数，就是控制其他变量，此变量的对数优势比。利用直线近似概率变化的简单解释。控制其他变量时，xix_i 变化一个单位相当于 π^\hat{\pi} 近似变化了 βj^π^(1−π^)\hat{\beta_j}\hat{\pi}(1-\hat{\pi})直接利用概率公式的解释。为了预测变量xjx_j 的效用，可以将其他的变量设定为样本均值，并给出最大与最小的 xjx_j 处的 π^\hat{\pi} ，通过 π^\hat{\pi} 或者 π^\hat{\pi}的差值对效应进行概括。但由于这样的概括对离群值很敏感，为了得到更稳健的概括，通常使用xjx_j的四分位数。对于具有不同单位的定量预测变量效应的比较。将这些预测变量全部减去各自方差，除以各自标准差，得到标准化预测变量，再进行回归。标准化预测变量每改变1个单位，等于原始预测变量改变一个标准差。每个回归系数代表了控制其它变量时预测变量1个标准差改变的效应。预测变量的标准化效应估计等于未标准化效应估计乘以标准差。