内容目录

什么是统计学，什么是描述统计，什么是推断统计统计研究的步骤描述统计

当我们信心满满，决定在数据分析的道路上再丰富一下自己的统计学知识时，映入眼帘的是一脸懵逼的复杂公式，看着就难受，也就是还没开始就放弃了的统计学，成了我们的一块不可触碰的隔离区，其实统计学并没有那么难，我们生活中随处可见，而且学习统计学，也不一定要会很多公式的推导，我们首先是先理解，从应用角度，然后再慢慢深入研究，毕竟我们不是搞科研的，懂并且会用是我们的第一步，那接下来我们就尽量不跟公式见面的情况来重新认识一下统计学。

聊一聊我们生活和工作中比较搞笑的统计学

1.你的工资被平均了吗？ 2016年国家统计局发布的工资数据中提到： 信息传输、软件和信息技术服务业平均工资得以快速增长，2016年平均工资为122478元，比上年增长9.3%

1.什么是统计学，什么是描述统计，什么是推断统计

统计学（statistics）：收集、处理、分析、解释数据并从数据中得出结论的科学。描述统计（discriptive statistics）:研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。

描述统计其实就是对数据进行总体特征的概述，例子：说一下班级这次考试的情况如何推断统计（inferential statistics）:是研究如何利用样本数据来推断总体特征的统计方法

推断统计其实是建立在描述统计的基础之上，在对总体数据有了大致的了解之后，运用一些分析方法，对数据进行预测，并达到统计决策的目的，其实不管是在统计学上，还是在实际的业务分析中，我们做分析的终极目的就是用来得出我们结论，应用于决策。例如：房价预测，通过预测数据来进行销售，用户看到房价走势，如果一路走高，是不是要提早下手。

2.统计研究的步骤

设计

全过程最关键的一步，良好的开端是成功的一半 选题--明确研究目的--提出假设--明确总体范围--确立观察指标--控制研究中的偏移--给出具体的研究方案

收集

收集数据，来源数据库，问卷等

整理

数据整理非常重要，现在的数据处理工具也比较好用，一定要把数据清洗干净，数据清洗好了才能得出正确的结论

分析

统计描述：了解样本数据的情况，是全部工作的基础，是尽量精确、直观而全面的对所获得的样本进行呈现

统计推断：从样本信息外推到总体，以获得对所感兴趣问题的解答

参数估计：样本-->所在总体特征

例： 该配件的日平均用量是多少？

3.描述统计

案例： 某仓库负责某地区售后维修服务所需配件的中转存储，每日该地区的业务员都会根据当天接单情况，从仓库中领取一定数量的各类配件。 现有某配件A在过去一段时间中每日实际领用量，希望据此了解该配件的日常消耗状况，以便为优化仓储提供支持。

使用频数表来观察数据的整体分布情况，比较直观，但有点粗糙

使用spss实现如下图形

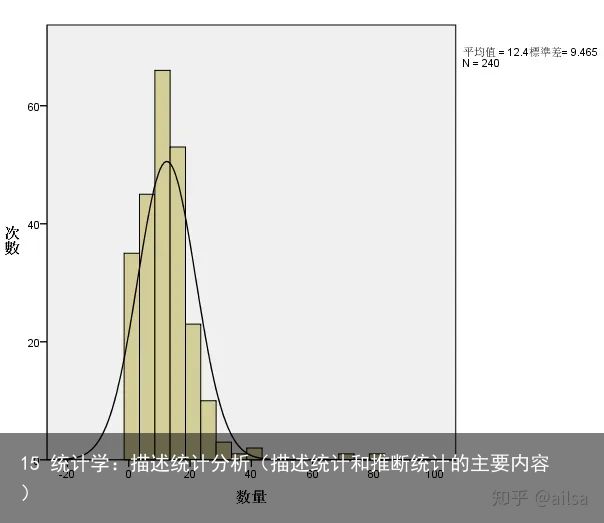
从图中我们可以获取什么？

集中趋势

高峰组段在什么位置

离散趋势

数据分布范围是什么，分散程度如何

分布形状

是否对称，分布曲线的形状

正负偏

分布特征

偏态 峰态

集中趋势

均数（mean）

描述一组数据在数量上的平均水平

总体均数和样本均数的符号

均数的优点：

高度浓缩了数据的精华，使大量的观测数据转变成一个代表性的数值。比较敏感，数据任何一个值发生变化，均数都会随之改变。大家熟知、都比较喜欢用、便于比较和传播

均数的缺点：

大锅饭：把各个观测数据之间的差异性掩盖了均数受极值的影响很大

举个例子，还是工资

每月工资

张三 3000 李四 4000 王五 5000 马云 40000

四人的平均工资：13000

我去，这么一算，大家工资都还不错啊，实际上呢？

这个均数毫无意义，既不能反映前三个人的工资，也不能体现马云的工资

因为他们的薪资差异过大，属于不同层级的，应该区分成两个总体去分析。

均数的适用范围

对称分布，特别是正态分布的数据，对于极端性数据均数绝对不适用

中位数（Median）

在均数不好用的时候，我们可以考虑使用中位数

将全体数据从小到大排列，在整个数列中处于中间位置的那个值就是中位数

个数为奇数的中位数

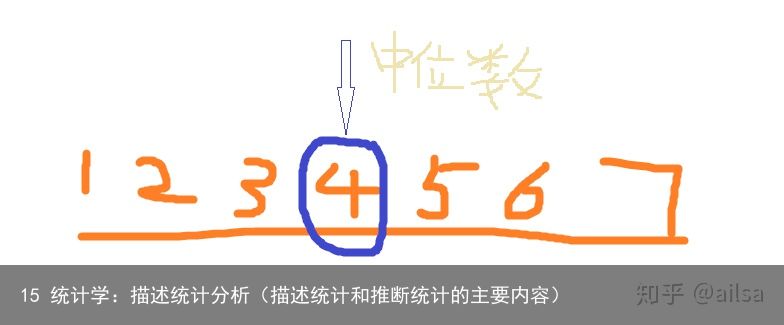
个数为偶数的中位数

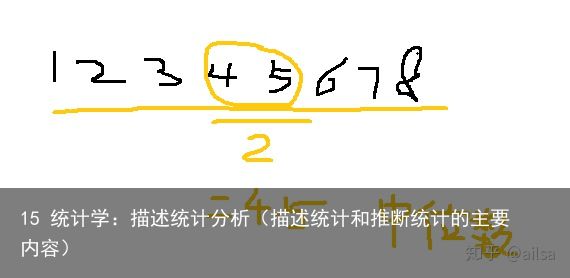
中位数的优点：

不受极端值的影响，在具有个别极大或极小值的分布数列中，中位数比均数更具有代表性，如上面例子，用中位数则是4500，至少代表了前三个人的工资水平

中位数的缺点：

不是所有人都能理解

损失信息：只考虑居中位置，其他变量值比中位数大多少或小多少，它无法反映出来，所以我们也是只能看到部分信息。

中位数的应用场景：对于对称性的数据，优先均数，仅仅对于均数不能使用的情况才使用中位数加以描述。

众数

一组数据当中，出现次数最多的那个数，工作中用的很少

回到刚才的案例中

提问：消耗量的平均水平应当用什么指标描述？

它不符合正态分布，使用中位数更合适

Excel怎么操作

使用函数，还有更方便的操作，讲完离散趋势再说

均数：average()

中位数：median()

众数：mode()

离散趋势

提问：如果用平均数来代表样本平均水平的话，对个体而言，什么指标可以代表其离散程度大小

离均差：x-μ

个体偏离均值的程度

提问：可否用离均差的总和来表示整个样本的离散程度

不可以，离均差有正负之分，加和会抵消为0

那怎么办，怎么解决正负号的问题？

可以考虑绝对值

but这种方式不便于计算

该怎么办，怎么找到一种既好算，又能处理正负号的问题？

求离均差的平方和

but 如果比较两个样本的离均差，一个样本量是10个，一个是1000个，实际上二者的离散程度是一样的，但是因为数量不同，造成平方和相加和数值差异很大，这该怎么办？

显然，我们发现离均差平方和的大小跟样本量有关

如果我们能够把离均差平方和/样本量，是不是就解决了这个问题

那其实这个就是方差的概念

总体方差公式

总体标准差

方差开根号，是我们日常生活中常用的代表离散程度的指标

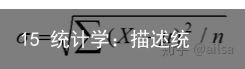
但是在实际的工作中，我们对于总体的数据往往是无法获取的，所以通常是通过随机抽取部分样本数据进行计算，因此公式稍微有点差别

样本标准差

举个栗子

某仓库比较配件A领用量与维修服务费的波动程度（离散程度）大小 数据汇总如下： 配件A： 均数 13.5件 标准差 7.6件 维修费：均数 247.9元 标准差 120.7元 如果配件A与维修费的波动程度是接近的，说明你领取了多少配件，收取了多少维修费，比较统一合理， 但是如果不一样，则说明维修费收取存在不合理，例如：打折过猛或者收费过高，那我们该怎么比较呢？ 直接比较标准差，这个貌似没有可比性吧，怎么办呢？

存在的问题：

1.测量尺度的相差太大：例如蚂蚁和大象的体重变异

2.计算单位不同：比较身高和体重的变异程度

那怎么办?

变异系数可以解决这个问题

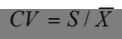
变异系数 = 标准差/均值

变异系数解决了不同样本变异程度对比的问题

配件A的变异系数 = 7.6/13.5 = 0.562963

维修费的变异系数 = 120.7/247.9 = 0.48689

二者有一定差异，但是差的不多，还算保持一致

方差-标准差-变异系数 应用场景

以均值作为集中趋势代表值，因此适用范围也受到相应的限制

本质上只适用于正态分布的数据资料

那问题来了，对于非正态分布的该咋办？我们上面讲了，集中趋势对于非正态分布可以使用中位数，那离散趋势呢？

我们可以使用百分位数

是一个位置指标，用Px表示，一个百分位数Px将一组观察值分为两部分，理论上有x%的观察值比它小，有（100-x）%的观察值比它大，适用于各种分布

常见的四分位数

P25、P50和P75分位数分别称作下四分位数，中位数 上四分位数

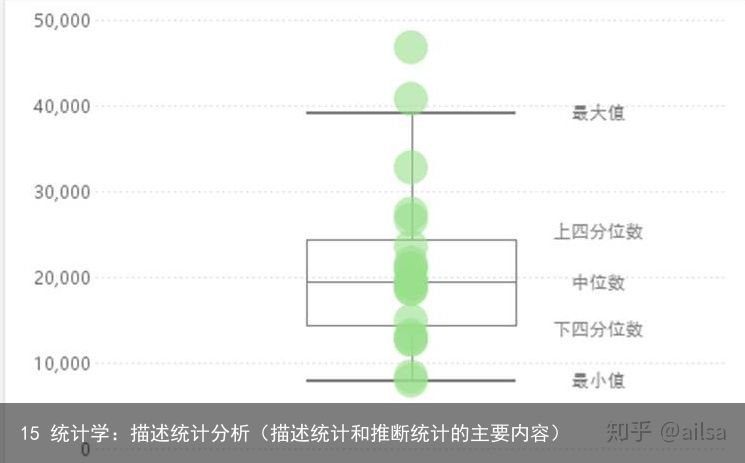
正好将样本值四等分，四分位数间距既排除了两端极端值的影响，又能够反映较多数据的离散程度。

回到刚才的案例中

提问：消耗量的离散程度应当用什么指标描述？

四分位数，因为不是正态分布

Excel怎么实现

使用函数

方差：var.s(num1,num2,....)

标准差：stdev.s(num1,num2,....)

变异系数：标准差/均值

百分位数：percentile.inc(array,k)

四分位数：quartile.inc(array,k)

分布形状

针对某种分布进行进一步的特征描述，常见的是用于正态分布的两个指标

偏度系数 正态 正偏态 负偏态峰度系数 正态 平阔峰 尖峭峰

Excel怎么实现

使用函数

偏度：skew()

峰度：kurt()

实现方式

使用分析工具

but 有些同学却找不到【数据选项卡】--【数据分析】的那个按钮，操作静止在了第二步，这可咋整，没关系的，这个数据分析工具默认是不显示的，需要后台设置一下，很简单，老师带你做

step1：点击【文件】--【选项】

step2: 【加载项】-- 【转到】

step3：勾选分析工具库--确定

总结：

用一张图来总结描述统计的重点知识

图表在之前的课程中已经讲过，这里就不详细赘述

今天得到描述统计就到这里啦，下篇文章给大家简单介绍推断统计的内容