探索性数据分析（EDA）是定量分析检测工作

包括用于揭示数据的信息技术和数据可视化方法，以及了解生成数据的过程。EDA是理念，数据应首先在概率模型、误差分布、变量关系等不做任何假设下进行探索，以发现揭示现象的信息。

关键点：作图，读图

目标：

为生成数据的过程确定合理的模型找出样本可能的异常值

一、探索单变量数据

1.直方图：

总结数据分布的一般特征，如形状、分散或位置

建议可能的概率模型

确定异常行为

主要有：

频率直方图

相对频率直方图（高度变为相对频率）

密度直方图（标准化，使面积为1）

2.茎叶图

若每个观测值至少包含两位数，可构建茎叶图

把每一次测量分成两部分：茎（守卫数字）和叶

茎列在垂直线的左侧，与该茎想对应的叶列在右侧

每个茎可有多行/叶，一次发现更多的信息

3.分位数图Quamtle-Based Plots

实际上，我们想知道数据是否以同样的方式分布

重要应用：比较两个分布/样本

进行数据分析之前，检查模型假设，如正态分布

尝试确定生成数据的分布，用于monte carlo模拟

优点：不要求两个样本有相同位置和比例参数

a：Q-Q图（分位数-分位数图）

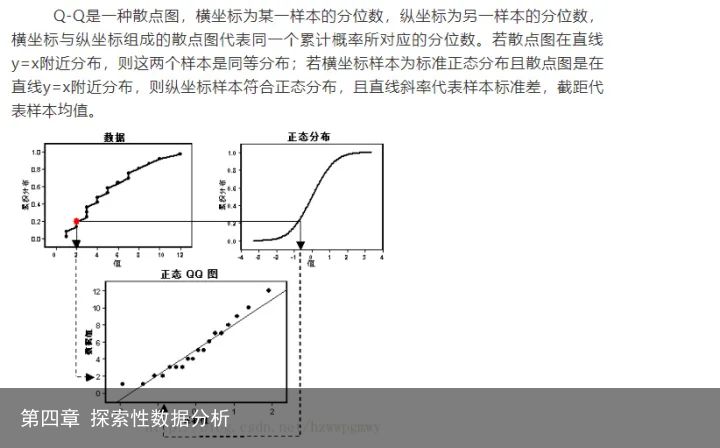
b：分位数概率图

连续分布：

总体分位数与样本的有序统计量相对应

在一个轴上，绘制了Xi

在另一个轴上我们绘制

C：离散分布

泊松图

离散数据是整数值，通过计算某事物发生次数来获得

频率分布数据含可能的计数值k和等于k的观测数

通过在水平轴上绘制计数值k和在垂直轴上绘制：

二项式图

D：箱线图（box plots,by Tukey，由两极限，三个分位数值确定）

IQR指四分位距

相邻值

在（LL,UL）中最极端的观测值

如果没有潜在的异常值，则相邻值就是最大和最小数据点

异常值

超出LL和UL的观测值，远离其余数据的样本点，其为适合进一步调查的采样点。

二.探索二元、三元数据

借助笛卡尔坐标，我们可以看到三维。

1.二元数据：

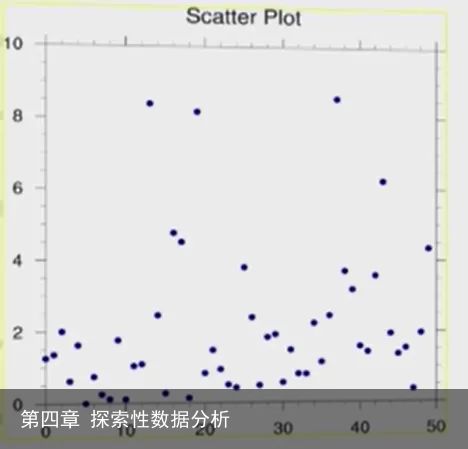
1.1散点图

其将有序对显示为点来获得，传达的信息：两变量之间的关系。

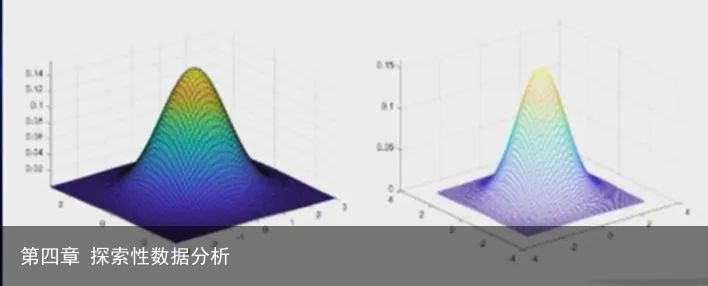
1.2曲面图

当数据表示为二元函数，其值视为曲面

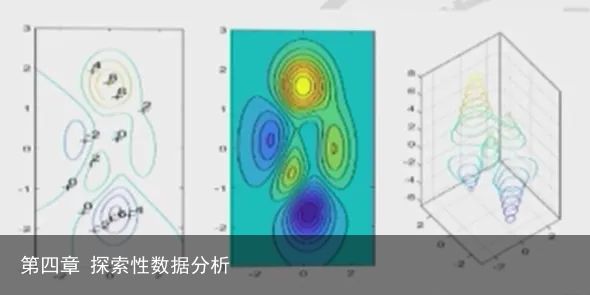
1.3等高线图

显示与地形图相似的恒定表面值线

1.4二元直方图

单变量密度直方图——我们的数据是如何分布的

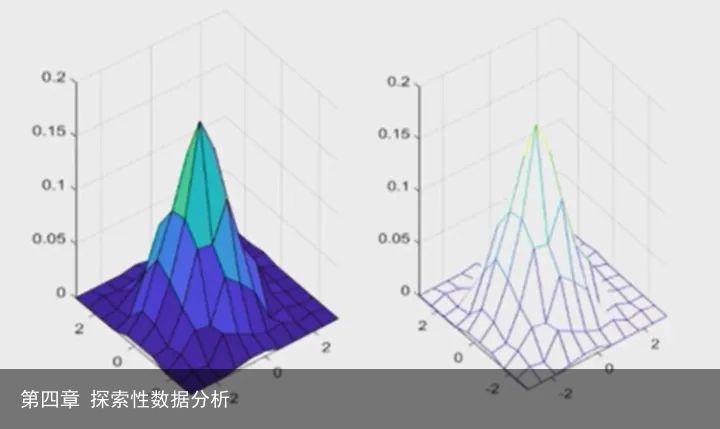
2.三元数据：

2.1三维散点图

三、探索多维数据

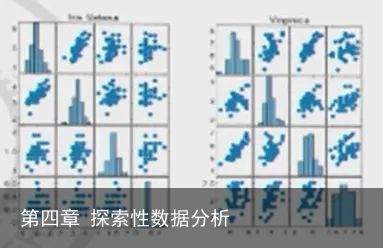
1.散点图矩阵

通过查看所有可能变量对的散点图，可以将其拓展到多维数据

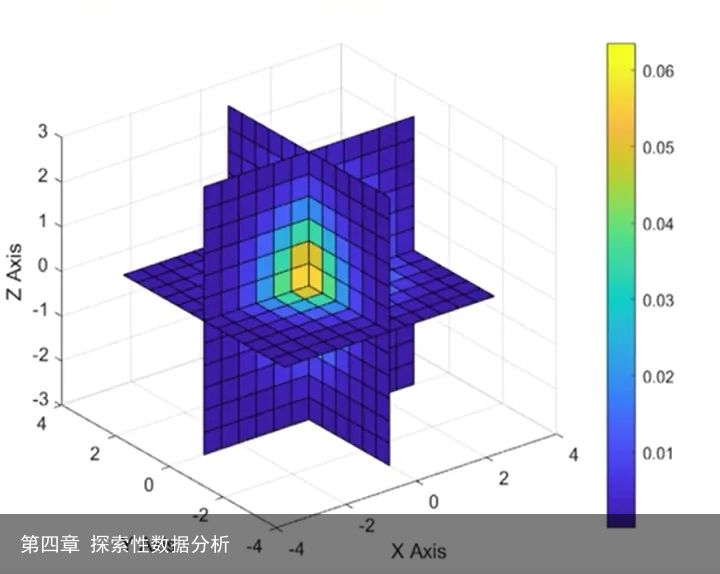
2.切片图和等值面

适用在体积上定义的概率密度函数情况。等值面是常数的曲面。

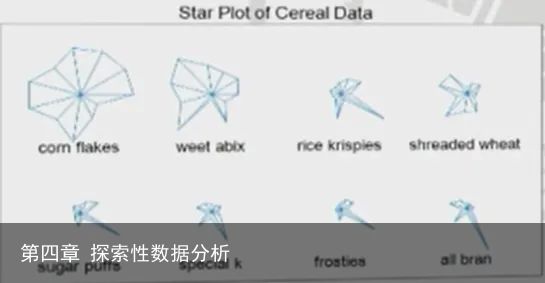
3.字形符号（手绘-小型数据）

3.1星图

样本中的每个观测数据点绘制为一个星，每个测量值显示为从公共中心点发出的径向线。

每个测量值都被绘成一个辐条，他与测量变量的大小成比例，辐条的末端与线段项链，形成一个星形。

星图是查看所有维度上的整个数据集的好方法，但不适合大量观测（n>10）或多个维度（d>15）。

3.2切尔诺夫脸图

用卡通脸来表示d维数据的方法。鼻子、眼睛、嘴、面部轮廓、眉毛等的大小和形状将由测量值决定。

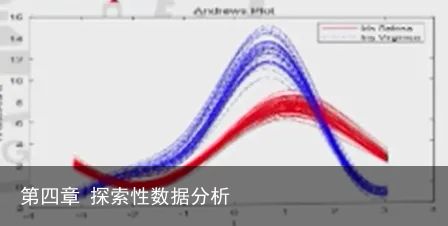
4.Andrews曲线

将每个观测值映射为一个函数。

类似于星图或Chernoff脸图，每个观察点/采样点都由一个字形表示，但在本例中，字形是一条曲线。

曲线的函数定义

其中t取值在（-Π，Π），x由变量个数决定。

每个观测值通过正弦和余弦投影到一组正交基函数上。

Andrews曲线保持均值、距离（常数倍）和方差Andrews曲线接近，相应的数据点也将接近。因此，其可用于寻找数据聚类。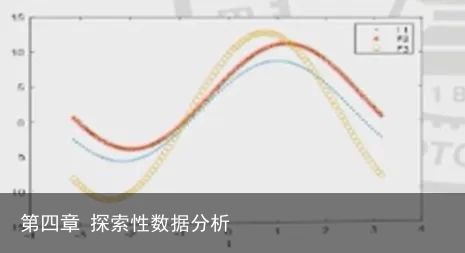

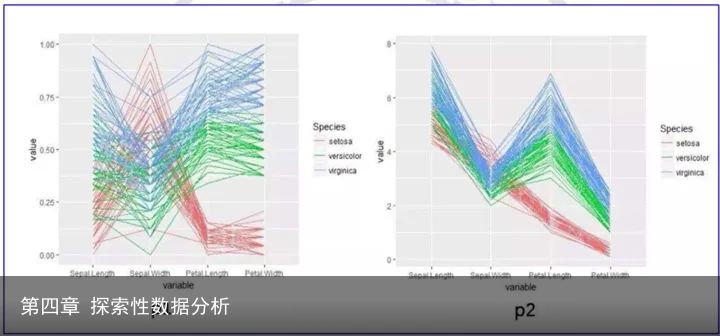
5.平行坐标图

与Andrews曲线一样，用于寻找数据聚类。