本文来阐述统计学基本的描述性统计分析在SAS软件内的实现方法与案例解读，首先大概过一遍统计学基本的描述性统计。

描述性统计就是利用手里已有的数据，分析数据的集中趋势和离散趋势，总体来说在统计学内数据可以分为以下三种类型：

一：分类数据，又名定性数据或者品质数据。这是一种非数字型数据。比如人口按照性别分可以分为男、女，企业可以按照行业属性分为：互联网企业、医药企业、家电企业等等。当然日常统计中为了方便起见，我们可以将这些变量赋予一个不支持加减乘除运算的数字(这儿说的不支持是因为对其进行加减乘除没有什么实际意义)，例如人口按照性别分类中我们可以将男记为0，女记为1(当然反过来男1女0也是可以的)。

二：顺序数据。它是分类数据的一种，但是！！！它的变量是有顺序的，或者说它的变量是有重要和不重要之分的！！ 例如，一个学生的考试成绩我们可以用：优、良、中、及格、不及格来表示，这儿有着明显的主次顺序，即优>良>中>及格>不及格（当然你想反过来不及格<及格...）也没问题。同样在日常的统计中，为了方便(反正就一个原则，怎么方便怎么来),将其赋予一个不支持加减乘除运算的数字，优——1，良——2，中——3，及格——4，不及格——5。

三：数值型数据，又名定量数据，其变量为数值形式的变量。故名思意，这是一种数值数据。而数值型数据中的变量又可以分为两类：

1，离散型变量

这些变量一般以整数的形式出现，可以一一列举。举个简单的例子：不同城市的企业数量，这些数据一定是数值型数据，这就是离散型变量，它的特点是你只能取它的整数值，也就是说你可以说其中一个城市有100家企业，但是你要是说这个城市有100.5家企业，这就没有什么意义了，因为我们都知道0.5家企业这是不存在的。同理的还有产品数量、汽车产量等等。

2,，连续型变量

与离散型变量相对应，这些变量可以取小数部分。比如一个城市所有人的平均身高，它可以是175cm，也可以是175.1cm或者175.2cm，这都是没问题的。这一类连续变化的变量我们就称之为连续型变量。

接下来介绍数据集中趋势和数据离散趋势的度量方法。

一：数据的集中趋势

1，众数：一组数据中出现最多的变量即为众数。

2，分位数：常用的有中位数（即二分位数）、四分位数、百分位数等，定义为分位数(n分位数)通过n-1个数据点将我们的数据平均分为了n份

3，平均数：平均数可以分为三类

1）简单平均数：公式为

2）加权平均数（针对分组数据），公式为

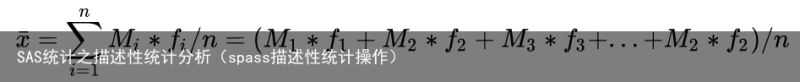
这儿的 Mi 指的是分组数据第 i 组的中位数, fi 为频数

3）几何平均数，公式为

众数，中位数，平均数之间显示数据的集中趋势与分布，如下图所示

二：数据的离散趋势

离散趋势，就是数据的分散程度，一下按照数据类型进行阐述

1.分类数据

分类数据的集中趋势可以使用众数来表示，离散趋势也与众数有关，统计学内有一个名为异众比率的值来描述我们分类数据的分散程度。定义如下：

异众比率指的是总体中非众数次数与总体全部次数之比，常常使用Vr来表示

假设我们有N个样本值，样本存在一个众数c，且众数的个数为n，则我们的异众比率

当N不变时，众数的个数（频数）n越大，异众比率越小，数据越往众数这个值集中。

2，顺序数据

顺序数据由于存在众数与分位数两种集中趋势的度量，故而我们可以使用异众比率来描述其离散趋势，也可以使用四分位距来表示数据的离散程度：四分位距（interquartile range, IQR），又称四分差。是描述统计学中的一种方法，以确定第三四分位数(上分位数)和第一二分位数(下分位数)的区别。

箱线图形状如下图所示：

上图中我们可以得到如下信息：

由于我们的四分位距IQR中集中了我们50%的数据，因此箱线图的宽度越大（IQR越大），则我们的数据越分散，因此图中数据相对较为集中；

上边缘到中位数距离小于下边缘到中位数距离。由于中位数是位置统计量，其值永远在数据的中间，因此图中数据很明显呈现了左偏分布

图中存在一个异常点，其值小于

3，数值型数据

1）极差：一组数据的最大值与最小值之差称为极差，也成为全距，用R表示

2）方差和标准差方差：各变量与其平均数离差平方的平均数，其中样本方差用

，总体方差用

标准差为方差开方，

3，标准分数：一组数据中各数值的相对位置。比如，如果某个数值的标准分数为-1.5，就知道该数值低于平均数1.5个标准差

4，经验法则与切比雪夫不等式

对于对称分布的数据，经验法则告诉我们：

约有68%的数据在±1个标准差范围内

约有95%的数据在±2个标准差范围内

约有99%的数据在±3个标准差范围内

对于偏态分布的数据，我们根据切比雪夫不等式可知至少有

的数据落在±k个标准差范围内,其中k>1的整数：

至少有75%的数据落在±2个标准差范围内

至少有89%的数据落在±3个标准差范围内

至少有94%的数据落在±4个标准差范围内

5，相对离散系数（变异系数）：对于平均水平不同或计量单位不同的多组数据间比较离散程度时，应使用离散系数

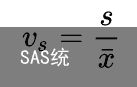
例如：已知某良种猪场长白成年母猪平均体重为190kg，标准差为10.5kg，而大约克成年母猪平均体重为196kg，标准差为8.5kg，试问两个品种的成年母猪，那一个体重变异程度大。

此例观测值虽然都是体重，单位相同，但它们的平均数不相同，只能用变异系数来比较其变异程度的大小。

由于，长白成年母猪体重的变异系数：10.5 / 190 * 100% = 5.53%

大约克成年母猪体重的变异系数： 8.5 / 196 * 100% = 4.34%

所以，长白成年母猪体重的变异程度大于大约克成年母猪，故而养殖大约克成年母猪风险更为稳定。

三 下面我们阐述统计学的描述性分析怎么在SAS内实现

1，means过程：数据集fiah包含了一个湖泊内的各种鱼类身长，重量，宽度等特征的样本，一共有7个变量，变量Species表示鱼的种类，Weight表示鱼的重量，Length1，Length2，Length3表示三种测量方法下的身长，Height表示鱼的宽度，现在计算各个数量指标的均值，中位数，众数，标准差，方差，变异系数和四分位数极差，部分数据表如下图

SAS代码为：

proc means data=sashelp.fish means std var cv range qrange;

title "Descriptive Statistics of Dispersion";

var weight length1 length2 length3 height width;

run;

代码结果如下

查看不同种类鱼的重量均值是否存在差别，代码为：

proc means data=sashelp.fish mean;

title "Descriptive Statistics of Tendency Using Class";

var weight;

class species;

run;

引入分类语句class，结果如下：

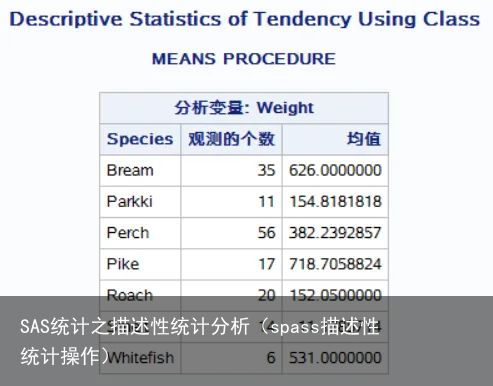
2，univariate过程：该功能与means功能一致，除此之外，还可以绘制直方图，更直观的得出变量的分布情况，一般语法如下：

Proc univariate data=数据集；

Var 分析变量；

Histogram 分析变量；

Probplot 分析变量；

Inset 统计量关键词；

Run；

其中：

var语句用来分析指定变量，如果没有var语句，系统将分析所有数值型变量

Histogram语句针对特定的变量绘制直方图，也可以使用选项 normal做出正态分布图

Probplot语句可以指定做出概率图，比较数据是否符合某一已知分布，如正态分布，二项分布，泊松分布等

Inset语句可以在univariate过程做出的图形上编著统计量计算量

举例：查看数据集fish中种类为Bream的鱼类宽度是否接近正态分布，代码如下：

proc univariate data=sashelp.fish plot ;

where species="Bream";

title "Descriptive Statistics Using Proc Univariate";

var height;

histogram /normal(mu=est sigma=est) kernel;

/* probplot/normal(mu=est sigma=est);*/

inset skewness kurtosis/ position=ne;

run;

代码结果如下图

分析报表发现：

1）数据均值为15.18，和中位数14.95很接近，说明该种类鱼的宽度分布基本是对称的

2）偏度系数为0.2417，说明该发布有轻微又偏的趋势

3）峰度系数为—0.5914，说明相较于正态分布，该分部的峰部较为平缓，没有厚尾特征

4）从正态概率图可以看出，散点基本在拟合的直线周围，说明该分布符合正态分布

5）直方图可以看出，大概45%的数据在中间的两个矩形中，该分布也比较近似符合正态分布

6）最后做了正态分布的检验，在后续假设检验中在详细讲解

本文讲解了统计学基本的描述性统计分析在SAS软件内的实现方法与案例解读，下篇文章将讲解参数估计和假设检验的概念