【免责声明：本文用于教学】

时间序列分析ⅡI——ARIMA模型

随着对时间序列分析方法的深入研究，人们发现非平稳序列的确定性因素分解方法（如季节模型、趋势模型、移动平均、指数平滑等）只能提取显著的确定性信息，对随机性信息浪费严重，同时也无法对确定性因素之间的关系进行分析。

而非平稳序列随机分析的发展就是为了弥补确定性因素分解方法的不足。时间序列数据分析的第一步都是要通过有效手段提取序列中所蕴藏的确定性信息。Box和Jenkins使用大量的案例分析证明差分方法是一种非常简便有效的确定性信息的提取方法。而Gramer分解定理则在理论上保证了适当阶数的差分一定可以充分提取确定性信息。

PROC ARIMA过程

ARIMA过程采用Box-Jenkins方法建立模型，是集一元时间序列模型判定、参数估计和预测为一体的多功能综合工具。当ARIMA模型包括其他时间序列作为输入变量时，有时也被称为ARIMAX模型。ARIMA模型还支持干预或中断时间序列模型、误差的多元回归分析、任意复杂程度的有理转移函数模型。

基本语法：

proc arima data=数据集 out=输出数据集;

where 条件表达式;

identify var=变量(…) <选项列表> ;

estimate <选项列表>;

forecast <选项列表>;

说明：

（1）where语句

指定用于分析的时间间隔，通常条件表达式是有关日期变量的条件表达式，例如：’31dec98’d < 日期变量 < ’31dec99’d

（2）identify语句

主要完成时间序列的差分计算，样本ACF、IACF和PACF函数的计算、卡方检验统计量和白噪声自相关检验的p值的计算。主要选项：

 var=变量(d1,…,dk)——是必选项，指定要分析的时间序列变量，按括号内列出的差分周期列表来计算时间序列的滞后差分。例如：var=X(1) 为对滞后1项的序列差分，即Xt-Xt-1;

var=X(2) 为对滞后2项的序列差分，即Xt-Xt-2;

var=X(1,1) 为X进行二阶差分，即(Xt-Xt-1)-(Xt-1-Xt-2); nlag=数字——指定计算自相关的滞后数，其值应大于p+d+q，小于观测数，默认值为24； crosscorr=(干预变量(d1))——列出有var=指定的响应序列的交叉相关变量。干预变量在交叉相关变量中。交叉相关变量的差分由圆括号内的差分滞后数确定。

（3）estimate语句

对已执行的identify语句中的响应变量规定一个模型，主要选项：

 p=(p1,p2,…)…(p1,p2,…)——定义一个在p中指定的滞后处具有自回归参数的模型，p的默认值为0; q=(q1,q2,…)…(q1,q2,…)——定义一个在q中指定的滞后处具有滑动平均参数的模型，q的默认值为0。如果p=和q=都没有指定，则拟合随机模型； noconstant——在模型中舍弃常数项μ; noint——在该模型中不拟合截距参数； method=ml | uls | cls——指定估计时使用的方法，分别为极大似然方法、无条件最小二乘法、有条件最小二乘法，默认为cls; outest=数据集——将参数估计值输出到指定的数据集； outmode=数据集——将模型和参数估计值输出到指定的数据集； outstat=数据集——将模型诊断统计量输出到指定的数据集； plot——可以绘制残差自回归函数等；

（4）forecast语句

利用estimate语句所产生的参数估计生成时间序列的预测值，主要选项：

 alpha=α——设置预测置信限的大小，上下置信限的置信水平为1-α，默认值为0.05; lead=n——指定要计算的多步向前预测值的次数，默认为24； back=n——指定在数据末尾前n个观测值开始进行分步预测，默认为0; interval=时间间隔——指定观测之间的时间间隔，常用的时间间隔为year、qtr、month、week、weekday、day、hour、minute、second; id=变量名——指明输入数据集中一个变量，用于识别与观测有关的时间周期； out=数据集——将预测值和其他值输出到一个指定的数据集中。

例1 有一组1949年至1961年国际航线旅客月度人数的记录：

YEAR123456789101112194911211813212912113514814813611910411819501151261411351251491701701581331141401951145150178163172178199199184162146166195217118019318118321823024220919117219419531961962362352292432642722372111802011954204188235227234264302293259229203229195524223326726927031536434731227423727819562842773173133183744134053553062713061957315301356348355422465467404347305336195834031836234836343549150540435931033719593603424063964204725485594634073624051960417391419461472535622606408461390432

使用ARIMA过程进行建模和预测。

（一）读入数据、绘制时间序列图、判断平稳性，代码：

运行结果及说明：

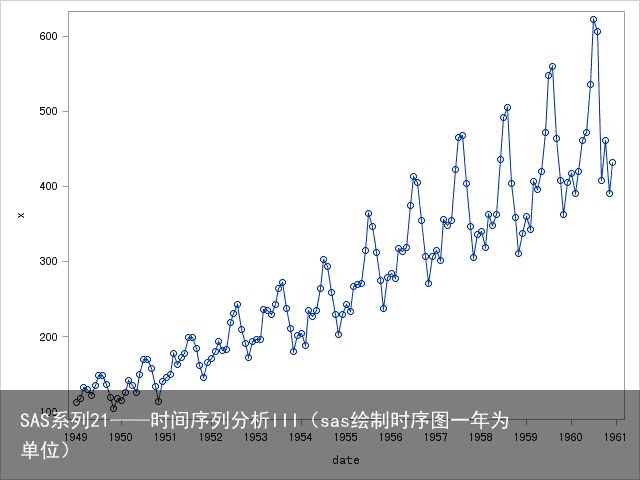
为了识别时间序列的数据是否平稳和是否明显有季节性，绘制时间序列图，可见不平稳。更精确的判断，通常利用proc arima过程的identify语句来检测序列是否平稳：

ARIMA 过程

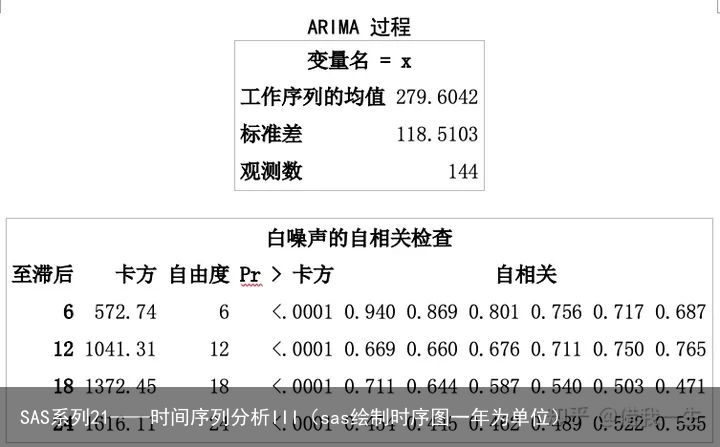
P值<0.0001<α=0.05，拒绝序列为白噪声的原假设，即序列是非平稳的。

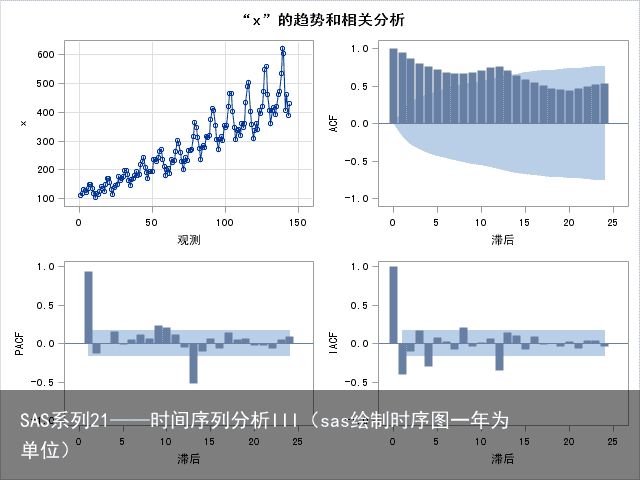
自相关系数ACF，发现自相关系数长期位于零轴正的一边，这是具有单调递增趋势序列的典型特征，同时自相关图呈现出明显的正弦波动规律，这是具有周期变化规律的非平稳序列的典型特征。自相关图显示出来的这两个性质和该序列时序图显示出的带长期递增趋势的周期性质是非常吻合的。

对于不同的时间序列类型，它们相应ACF的特性有：

①若时间序列是随机无趋势的，所有时滞的自相关系数都等于0;②若时间序列是上升或下降趋势的，那么对于短时滞来说，自相关系数大且为正，而且随着时滞lag的增加而缓慢地下降。ACF本身似乎随着时滞长度的增加而呈下降趋势;③若时间序列无趋势但具有季节性，那么对于按月(L=12)采集的数据来说，时滞12，24，…的自相关系数达到最大（即nL处），而随着时滞长度增加时，变得较小;④若时间序列有趋势且具有季节性，那么自相关系数特性类同于有趋势序列，但是它们是摆动的，对于按月的数据，在时滞12，24…等处具有峰态;⑤若时间序列是平稳的，它具有正自相关的误差项，那么低阶的自相关系数较大，但是随着时滞长度的增加而迅速地衰减;

另外，在ACF图中，通过自相关系数值是否在零点附近的两条对称的虚线之内，完成不同时滞的总体自相关系数为0的检验。

（二）变换不平稳序列为平稳序列

最常用的变换方法有：

①若时间序列呈线性趋势，均值不是常数，利用一阶差分将产生一个平稳序列；②若时间序列呈二次趋势，均值不是常数，利用二阶差分将产生一个平稳序列；③若时间序列呈现出随时间的上升或下降而偏差，方差不是常数，通常可利用取自然对数转化为平稳序列；④若时间序列呈现指数趋势，均值和方差都不是常数，通常也可利用取自然对数转化为平稳序列；⑤若时间序列呈现“相对环”趋势，通常将数据除以同时发生的时间序列的相应值转化为平稳序列。

一、取对数消除振幅变大趋势

从原始序列的时序图或ACF图发现，该序列具有季节性变化同时有增大的趋势，而且季节变化的振幅越来越大。因此，先对数据取对数来先消除增幅越来越大的现象。

代码：

data arimad02; set arimad01 ; xlog=log(x); run; proc print data = arimad02; run; goptions reset=global gunit=pct cback=white border htitle=6 htext=3 ftext=swissb colors=(black); proc gplot data=arimad02; plot xlog*date / vaxis=axis1 haxis=axis2 href=31dec1949d to 1jan61d by year; plot2 x*date /vaxis=axis3 vref=100; symbol1 i=join v=c h=3 l=1 r=1 font=swissb c=green; symbol2 i=join v=c h=3 l=1 r=1 font=swissb c=blue; axis1 label=(Log) order=(4.5 to 6.5 by 0.5) offset=(0,45); axis2 label=(12 Month) order=(1jan49d to 1jan61d by year); axis3 label=(Passenger) order=(100 to 700 by 100) offset=(23,0); format date monyy. ; title1 Time Serial Log Chart; run;

运行结果（为便于对比，按12个时间单位间隔画在同一图上）：

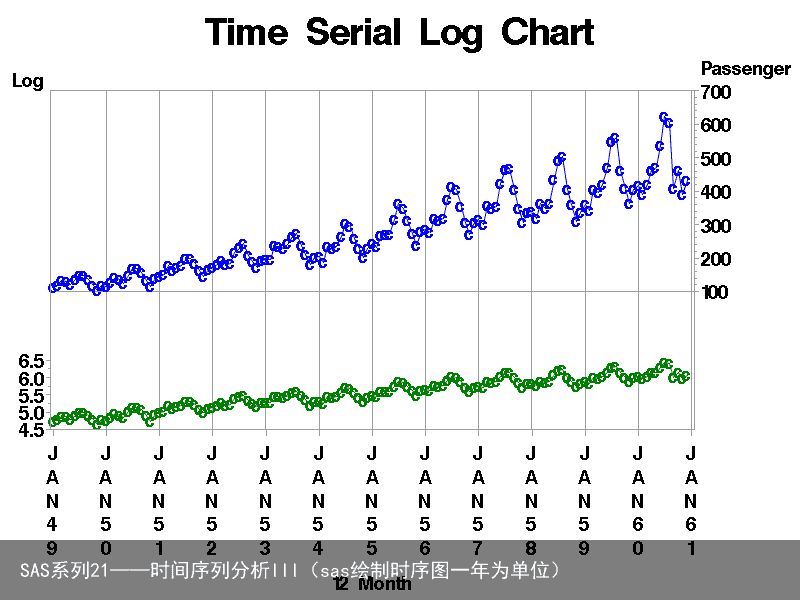
二、取两次差分消除季节增长趋势

对取对数后的序列，明显呈现季节性的增长的趋势，仔细分析每12个单位的周期还有增长趋势。所以需要对该序列再进行滞后一次和滞后12次共两次差分最终转换为平稳序列。

代码：

data arimad03; set arimad02; dif12=dif1(xlog)-(lag1(xlog)-lag12(xlog)); run; proc gplot data=arimad03 ; plot xlog*date /vaxis=axis1 haxis=axis2 href=31dec1949d to 1jan61d by year; plot2 dif12*date /vaxis=axis3 vref=-1; symbol1 i=join v=c h=3 l=1 r=1 font=swissb c=green; symbol2 i=join v=c h=3 l=1 r=1 font=swissb c=blue; axis1 label=(Log) order=(4.5 to 6.5 by 0.5) offset=(0,45); axis2 label=(12 Month) order=(1jan49d to 1jan61d by year); axis3 label=(Dif1-12) order=(-1 to 1 by 0.2) offset=(23,0); format date monyy. ; title1 Time Serial Dif Chart; run;

运行结果：

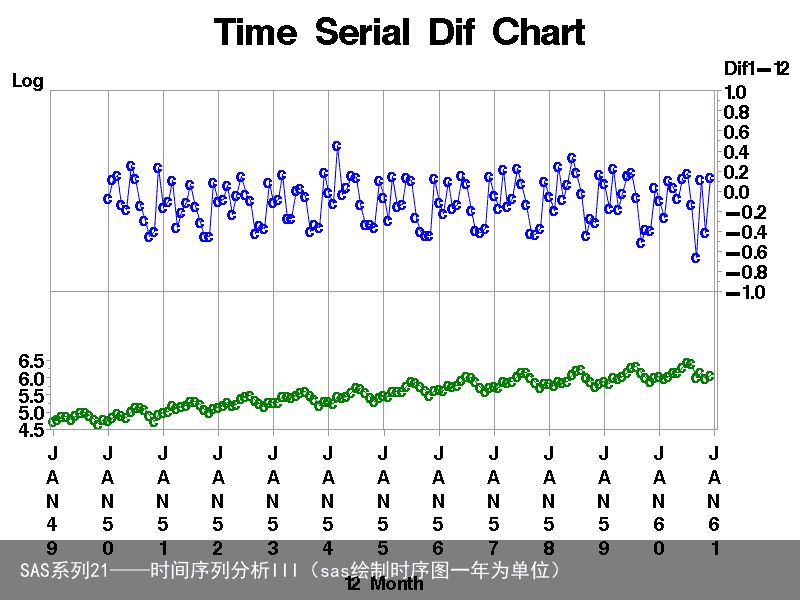
（三）检验待选的时间序列模型的自相关函数

对需要转换为平稳时间序列的数据，若最终是要用差分的方法来转换，通常可直接调用PROC ARIMA过程的identify语句来实现对指定变量xlog所选差分的时滞数（如1和12）的检验。

代码：

proc arima data=arimad02; identify var=xlog(1,12) nlag=15; run;

运行结果：

ARIMA 过程

ACF图中，自相关系数在延迟1阶后都落入2倍标准差内，然后在延迟12阶处突然有一个较大的自相关系数，紧接着又落入2倍标准差内，很象在1,12处截尾；又根据PACF图中，偏自相关系数很象在1,12处拖尾，在3和9处有超过2倍标准差，因此可选择MA的阶数为1,12。从IACF及PACF图看可选择AR的阶数为1,12。

自相关系数的白噪声检验，明显看出延迟6期和12期的QLB统计量分别为27.44和44.65，p值<α=0.05，拒绝序列为白噪声的原假设，即拒绝延迟期数小于等于6和12的序列值之间相互独立，说明经过滞后1次和滞后12次共两次差分转换后序列是平稳非白噪声序列，还蕴藏着相关信息需要提取出来，因此该序列蕴含ARIMA模型。

（四）估计备选时间序列模型的参数

代码：

proc arima data=arimad03; identify var=xlog(1,12) nlag=15; estimate q=(1)(12) p=(1)(12) noconstant outmodel=xmode; run;

运行结果及说明：

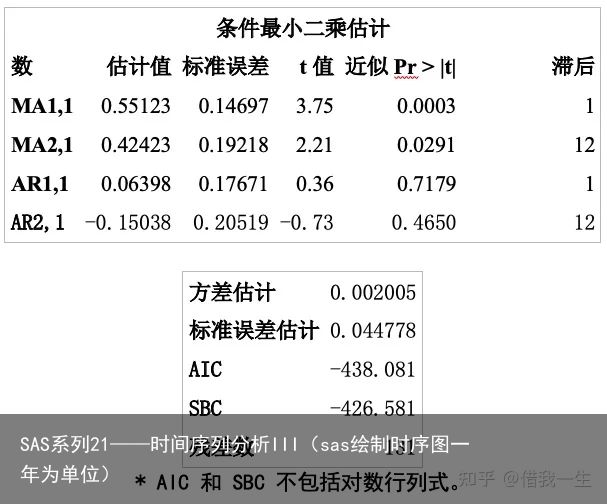
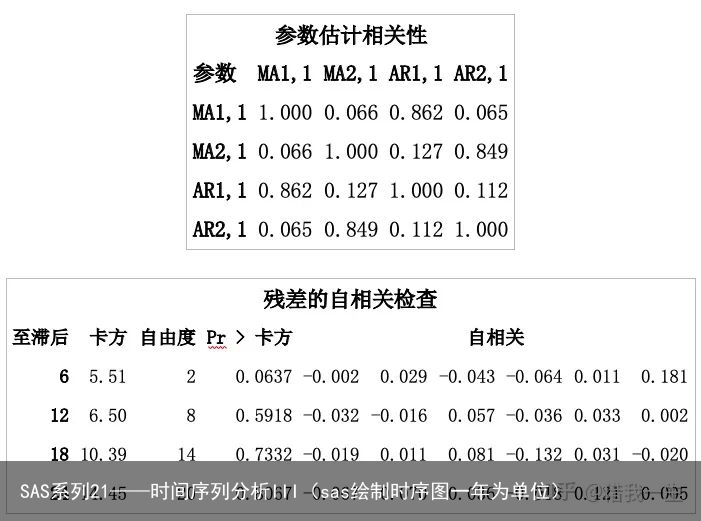
不带均值的条件最小二乘估计输出：该参数的估计值、标准误差和t值，以及该参数在模型中滞后数。

进一步诊断检验模型，若拟合的模型是可行的，则所有参数估计应该具有显著的t值，残差近似地为正态，残差序列具有随机无趋势序列的ACF与PACF，且不含有过度的p、d、q。

t统计量（其精确性依赖于模型的有效性和观察序列的长度等因素）用来检验该项系数是否为0. 拟合的ARIMA(1,1,1)×(1,1,1)12模型的具体形式为：

由于AR1,1及AR2,1的t值分别为0.36和-0.73（很小），所以该项系数为0的假设检验并不显著p值<α=0.05，故可以丢弃这两项。重新估计：

（五）估计模型参数、用模型进行预测

代码：

proc arima data=arimad03; identify var=xlog(1,12) nlag=15; estimate q=(1)(12) noconstant outmodel=xmode; forecast lead=12 interval=month id=date out=forxlog; run; proc print data=forxlog; run;

运行结果及说明：

参数估计的t值为6.58和5.54（较大），故要保留。拟合优度统计量表中给出了残差序列的方差、标准误差，以及按AIC和SBC标准计算的统计量，这两个值较小，表明对模型拟合得较好。

另外从-441.3195<-438.08143，-435.56911<-426.58065可看出本次拟合的ARIMA(0,1,1)×(0,1,1)12模型比上次拟合的模型要好。

估计值之间的相关系数为-0.064，这是一个较小的相关系数，如果这个相关系数较大时，就需要考虑是否删除其中一个参数。

对模型拟合后残差为白噪声原假设进行检验，延迟6期和12期的QLB统计量分别为5.60和6.54，相应p值=0.2312和0.7684>α=0.05，故不能拒绝拟合模型的残差为白噪声，说明这个拟合模型，延迟数小于等于6期和12期的所有残差自相关系数为零，即残差中蕴涵信息已经完全被提取出来了。

最后将表中移动平均MA的两个因子（1-0.50275B）和（1-0.52993B12）代入ARIMA(0,1,1)×(0,1,1)12模型得到：

其中，Z=log(xt).

预测今后一年（12期）国际航线各个月度的旅客人数，结果存在数据集forxlog中：

144DEC606.068436.057200.0445595.969876.144530.01123145JAN61.6.098730.0445596.011396.18606.146FEB61.6.041480.0497645.943956.13902.147MAR61.6.157260.0544746.050496.26403.148APR61.6.188070.0588086.072816.30333.149MAY61.6.221600.0628436.098436.34477.150JUN61.6.356990.0666356.226386.48759.151JUL61.6.496680.0702226.359046.63431.152AUG61.6.491720.0736356.347406.63604.153SEP61.6.209520.0768966.058806.36023.154OCT61.6.197880.0800256.041046.35473.155NOV61.6.051470.0830355.888736.21422.156DEC61.6.155650.0859415.987206.32409.

最后，将xlog预测值转换为原来的x值，并绘制带上下95%置信度线的原始数据线和预测数据线的时间序列图。

代码：

proc gplot data=arimad04; where date>=1jan57d; plot x*date forecast*date l95*date u95*date /overlay vaxis=axis1 haxis=axis2 href=31dec60d ; symbol1 i=join v=C h=2.5 l=1 font=swissb c=red; symbol2 i=join v=F h=3 l=1 font=swissb c=blue; symbol3 i=join l=1 font=swissb c=green; symbol4 i=join l=1 font=swissb c=green; axis1 label=(Passenger) order=(250 to 800 by 50); axis2 label=(Month) order=(1jan57d to 1jan62d by year); format date monyy. ; title1 Forecast Chart; title2 C--x; title3 F--forecast; title4 None--u95 and l95; run;

运行结果：