在对AB测试的实验结果进行分析之前，我们应该先简单了解一下AB测试的统计学原理——假设检验，AB测试的实验结果分析，实际上就是如何进行假设检验，并作出正确的决策，以下是正文：

1.假设检验

1.1 假设检验的定义

具体到A/B测试里的假设检验，就是指假设实验组的总体参数等于对照版本的总体参数，然后利用这两个版本的样本数据来判断这个假设是否成立。如果样本数据拒绝原假设，我们说检验的结果是显著的；反之，我们则说结果是不显著的。

1.2 假设检验的流程

了解了假设检验的流程之后，我们一一介绍一下这个里面的一些基本概念。

1.3 假设检验中的基本概念

1.3.1 原假设H0和备择假设H1

我们常把没有把握不能轻易肯定的命题作为备择假设 H1H_1 ，而把没有充分理由不能轻易否定的命题作为零假设 H0H_0 ，或者说我们将希望通过实验结果推翻的假设记为零假设 。

原假设和备择假设是一个完备事件组，而且相互对立。在一项假设检验中，原假设和备择假设必有一个成立，而且只有一个成立。

1.3.2 检验统计量

在AB测试涉及的假设检验中，我们所构造的检验统计量稍微有一丢丢复杂，因为假设检验想要比较两个总体参数是否存在显著差异，所以对应的两个样本的统计量相比单个样本的统计量复杂一些。但有了上一篇文章的推导之后，我们了解了tt 统计量是如何构造的，所以可以直接用一张图来表示不同情况下对应的不同统计量的形式。

2. 实验结果分析

当我们提出假设，并且构造完统计量之后，我们就要进行决策了，在统计学中，进行决策通常有两种方式：

一种是将统计量的值与给定显著性水平下统计量的分布的临界值作比较，以此来判断是否接受原假设。这种根据统计量落入的区域做出是否拒绝原假设的决策。确定显著性水平 α\alpha 以后，拒绝域的位置也就确定了。(显著性水平就是我们后文中要提到的犯第一类错误的概率)

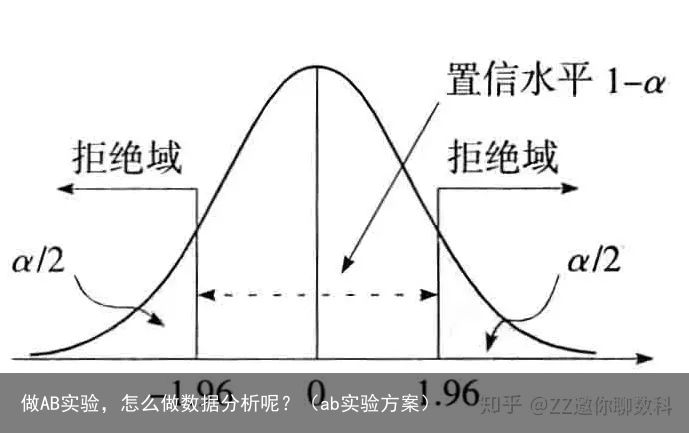
但实际进行AB测试时，我们使用的是以 PP值为主的实验结果评估体系。

2.1 PP 值

如果 PP 值很小，说明发生这种情况的概率很小，而一旦发生了，根据小概率原理，我们就有理由拒绝原假设， PP 值越小，拒绝的理由越充分。

举个例子：假设 H0:μ=0H_0: \mu=0,那我们随机抽取一个样本，其均值大于00 的概率就是 PP 值。

通常，我们将 PP 值与事先确定的显著性水平 α\alpha 进行比较，如果

第 I 类错误（弃真错误）：原假设为真时拒绝原假设；第 I 类错误的概率记为 αα ，也好就是我们前文提到的显著性水平。

第 II 类错误（取伪错误）：原假设为假时未拒绝原假设。第 II 类错误的概率记为β β 。

（2）统计功效

一般情况下，我们在做假设检验时候，希望拒绝原假设，得到新的结论。比如我们做AB测试，我们当然希望实验组的效果要好于对照组。也就是我们希望不要出现应该拒绝原假设时，我们却没有拒绝的情况，这就是刚才说的第二类错误。

统计功效 PowerPower 就是我们没有犯第II类错误的概率1−β1-β ，也就是原假设不成立时，被我们拒绝的概率。

实际进行AB测试时，统计功效就是，当两个不同版本之间存在显著差异时，实验能正确做出存在差异判断的概率。

该值越大则表示概率越大、功效越充分。一般来说，我们期待并设置的最低的统计功效值为80%。

2.3 置信区间

统计学中用样本去推断总体有两个工具：参数估计与假设检验。

这里我们稍加笔墨来介绍一下参数估计，目的是为了引出在AB测试中最关注的元素之一：置信区间。

参数估计和假设检验都是利用样本对总体进行推断。但是推断的角度有所不同。

参数估计是用样本统计量去估计总体参数，总体参数在估计前未知；

而假设检验，则是先对总体参数的值提出一个假设，然后利用样本统计量去检验这个假设是否成立。

参数估计又分为点估计和区间估计。

点估计，顾名思义就是用样本统计量的某个值作为总体参数的估计值。

区间估计，就是基于点估计，给出总体参数估计的一个区间范围，这个区间通常由样本统计量加减估计误差得到。这个区间也就是我们所说的置信区间, 我们给它一个官方的定义：

在上文构造统计量的表格中，已经列举出了置信区间的计算公式，这里我们也不过多的介绍了。

由于置信区间是一个估计区间，但是我们不能保证它一定包含总体参数。我们只能说构造的是一定置信水平下的置信区间。什么是置信水平呢？

举个栗子：

我们有100个样本，由100个样本构造了100个置信区间，其中有95%的区间包含总体参数，5%没有包含，这个95%就是置信水平。

介绍完置信水平之后，我们就可以用一张图来表示置信区间与置信水平：

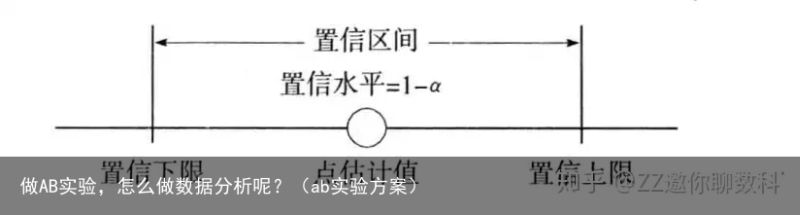
在实际进行AB测试时，置信区间可以辅助确定版本间是否有存在显著差异的可能性：如果置信区间上下限的值同为正或负，认为存在有显著差异的可能性；如果同时有负值和正值，那么则认为不存在有显著差异的可能性。

2.4 实验结果分析体系

所以，我们的实验结果分析体系就是由上述的PP 值、统计功效和置信区间所构成的。

（1）P值

判断两个不同版本的实验结果之间存在显著差异的概率。如果 p值<α（显著性水平，一般取0.05），就表示存在显著差异。

（2）统计功效

当两个不同版本之间存在显著差异时，实验能正确做出存在差异判断的概率。可以理解为我有多少的把握认为版本之间有差别。

（3）置信区间

置信区间可以辅助确定版本间是否有存在显著差异的可能性。

综上，我们认为当AB测试实验数据在95%的置信水平区间内，P值小于0.05，功效大于80%的情况下，实验结果是可信赖的。当然，这是一个严格的理想标准。在使用的实际过程中，我们会遇到多种情况，比如P值符合标准，功效还差一些，此时，我们就要根据实验背景与经验，具体问题具体分析。

3. 如何计算样本量

从理论上讲，样本量越多越好：

因为当样本数量很少的时候，实验容易被新的样本点带偏，造成了实验结果不稳定，难以得出确信的结论。

相反的，样本数量变多，实验说服性也更强。

但是在现实操作中，样本量应该越少越好，这是因为：

最小样本量是按照统计功效进行计算的，主要分两类：绝对值类（例如：UV）和比率类（例如：点击率）：

（1）均值类

均值类假设检验形式通常为：

H0:μA−μB=0H1:μA−μB≠0H_0:\mu_A-\mu_B=0\\ H_1:\mu_A-\mu_B\neq0

故对应的样本量计算公式为：

nA=κnB and nB=(1+1κ)(σz1−α/2+z1−βμA−μB)2n_A=\kappa n_B \;\text{ and }\; n_B=\left(1+\frac{1}{\kappa}\right) \left(\sigma\frac{z_{1-\alpha/2}+z_{1-\beta}}{\mu_A-\mu_B}\right)^2\\

其中，两组样本量之比为

κ=nAnB\kappa=\frac{n_A}{n_B}\\

统计功效的计算公式为： 1−β=Φ(z−z1−α/2)+Φ(−z−z1−α/2),z=μA−μBσ1nA+1nB1-\beta= \Phi\left(z-z_{1-\alpha/2}\right)+\Phi\left(-z-z_{1-\alpha/2}\right) \quad ,\quad z=\frac{\mu_A-\mu_B}{\sigma\sqrt{\frac{1}{n_A}+\frac{1}{n_B}}}\\

（2）比例类

均值类假设检验形式通常为：

H0:pA−pB=0H1:pA−pB≠0H_0:p_A-p_B=0\\ H_1:p_A-p_B\neq0

故对应的样本量计算公式为： nA=κnB and nB=(pA(1−pA)κ+pB(1−pB))(z1−α/2+z1−βpA−pB)2n_A=\kappa n_B \;\text{ and }\; n_B=\left(\frac{p_A(1-p_A)}{\kappa}+p_B(1-p_B)\right) \left(\frac{z_{1-\alpha/2}+z_{1-\beta}}{p_A-p_B}\right)^2\\

统计功效的计算公式为：

1−β=Φ(z−z1−α/2)+Φ(−z−z1−α/2),z=pA−pBpA(1−pA)nA+pB(1−pB)nB1-\beta= \Phi\left(z-z_{1-\alpha/2}\right)+\Phi\left(-z-z_{1-\alpha/2}\right) \quad ,\quad z=\frac{p_A-p_B}{\sqrt{\frac{p_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}}}\\

计算样本量的大小，是整个AB测试，实验设计中关键的一环，他可以决定最终实验结果的好坏。这部分内容节选自我的专栏文章：

对AB实验如何设计实验流程感兴趣的可以仔细阅读一下。

最后，觉得有帮助的可以点个赞奥~