辩证法中强调联系是普遍的，而如何判断两个变量之间是否存在联系呢，又如何衡量这种联系的程度呢？这就需要进行相关分析了。

什么是相关分析？

相关分析是测量变量之间是否存在相关程度的统计方法。我们通过相关分析可以确定是否存在相关关系，及相关关系的程度（通过相关系数表示）。

变量数量对相关的影响

提及相关分析，我们一般会想到两个变量之间的相关分析，实际上对于任何多个变量，任何类型的变量，都可以进行相关关系的考察。只不过使用的统计方法存在差别。

其中包括：

研究一个变量和另一个变量之间的相关关系研究一个变量和多个变量之间的相关关系研究两个变量群之间的相关关系研究多个变量群之间的相关关系

在此，我们仅讨论两个变量之间的相关关系情况，其他的内容我们接下来逐步讲解。

相关关系的类型

我们确定了研究相关关系的变量个数之后，还需要确定研究的两个变量的测度类型和相关关系的形式。测度类型我们之前已经有了了解，接下来我们探讨什么是相关关系的类型。

我们根据变量间的函数关系，把相关关系划分为两大类：

线性相关：两变量在表达式上呈现（直线）线性方程的形式。非线性相关：两个变量存在的线性趋势为曲线形式。

相关关系的方向

我们根据两个变量相关关系的方向，即同向还是反向，可以把相关关系分为以下：

正相关与负相关：如果 A 变量增加时 B 变量也增加，则称为正相关，如 A 变量增加时 B 变量减小，则称为负相关。

相关关系的强弱

如果两个变量存在相关关系，那么接下来我们就需要衡量两个变量相关关系的程度，我们一般使用相关系数来衡量相关的程度。

两变量的相关程度达到了可以通过精确函数表达的程度，当得知 A 变量取值时，就可以准确推算出 B 变量的取值时，我们程之为完全相关。完全相关又分为完全正相关和完全负相关两种。

今天，我们只讨论两个变量之间的相关关系的情况。根据两个变量的类型，我们可以使用不同的相关分析统计方法。

两个连续变量的线性相关关系：Pearson 相关系数

两个定序变量的相关关系（或不满足正态分布假设的等间隔数据）：Spearman相关系数、Kendall’s tau-b相关系数

我们使用最为广泛的相关系数是 Pearson相关系数，因此今天也就着重讲解Pearson相关分析。

Pearson 相关系数是定量的描述线性相关程度的指标。

什么情况下使用 Pearson 相关分析？

任何一种统计方法都是有适用条件的，对统计方法运用得好坏和正确不在于是否能写出公式或能否计算出结果，而在于针对数据特征懂得运用正确的统计方法。只有在以下情况中，才能使用 Pearson 相关分析：

变量：两个定距变量，且两个变量呈正态分布；

相关类型：确定是否存在线性关系及衡量其程度

同时，样本中存在的极端值对Person相关系数的计算影响极大，因此要慎重考虑和处理，必要时可以对其进行剔除，或者进行变量变换，以避免由一两个数值导致出现错误的结论。需要注意的是，有的时候在分别观察每个变量时极端值并不明显，但是联合观察两个变量时就会凸显出来。因此还需要满足：

确保样本中不存在极值（可以通过数据预处理去掉极值）

案例

研究问题与数据

中国消费者信心调研（CCSS）是一项针对中国地区的消费者对当前经济发展形势表现出的信心程度及其变动的一项调查，在此CCSS 案例的调查结果作为分析数据1。我们通过统计分析，考察年龄与信心指数是否存在相关关系。

SPSS 操作

我们打开 SPSS，导入数据后进行操作：【分析】【相关】【双变量】，将需要分析的变量选入“变量”栏目中，相关系数选择 Person（皮尔逊），其他保持默认。

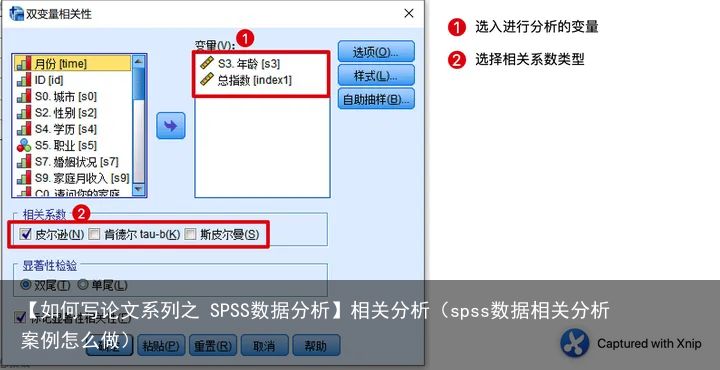相关分析相关分析

分析结果解读

相关分析结果

图中给出的就是相关分析的结果，我们分析了两个变量，因此结果为 2*2 的矩阵。每个单元分为三行，分别是相关系数、P 值和样本数。

要读懂相关分析，我们分为以下两个步骤：

观察“显著性（双尾）”，是否小于 0.05，若小于0.05，则在 0.05 显著性水平下，相关性显著；若小于 0.01，则在 0.01 显著性水平下，相关性显著；否则相关不显著，即可认为不相关。这一步实际上是相关系数的检验。

SPSS 进行相关性分析的时候，第一步是根据样本数据计算出相关系数，第二步是对计算出的相关系数进行检验，以确定其不是从一个数值为 0 的相关系数的总体中抽出的（避免计算出的数值是由于抽样误差所导致的），检验后得到 p 值，再将 p 值和临界值$\alpha $比较，判断相关是否显著。在相关性显著的前提下，观察 Person（皮尔逊）相关系数的大小，确定相关程度。根据相关系数的绝对值大小，确定相关程度：

0.1-0.3为弱相关

0.3-0.5为中等相关

0.5-1.0为强相关

结果撰写

本研究采用 Pearson 相关分析研究消费者年龄与信心指数的相关性，结果发现两变量呈现线性相关关系，Pearson 相关系数为-0.219.

消费者年龄与信心指数的相关分析

论文案例

我们选取如下论文作为案例进行说明：

王广新,王悦.支持智慧学习的语境化叙事游戏开发与学习效果验证[J].中国远程教育,2019(10):20-28+92-93.

文章为了研究智慧学习的语境化叙事游戏对学习效果是否有促进作用，对游戏叙事体验与发游戏化发现式学习效果进行了相关性分析，并给出了相关系数及假设检验结果，从中可以了解到各个研究变量之间的相关关系。

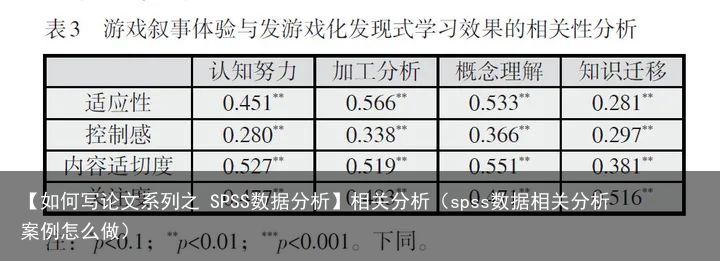游戏叙事体验与发游戏化发现式学习效果的相关性分析

[1] 案例数据选自张文彤：SPSS 统计分析基础教程（第 2 版）